とりあえずブログ始めてみました。
自分は数学とプログラミングを趣味をしている大学生です。大学生じゃなくなっちゃった…
よってそれらのことについてまあ適当に何か書ければいいかなと思っています。
ーーーー
内容に何かあれば(例:感想/これは間違ってる/ここが分かりにくい/etc...)以下に連絡ください
twitter: @shakayami_
またはマシュマロでもOK
大学院修士課程の「3」年間を振り返る
修士課程ってふつう2年間じゃなかった？
君のような勘のいいガキは嫌いだよ
すべて終わったらこれを書こうと思ってたので書く
何があったか3行で書きます
修士課程に進学！
しかしメンタルを病んでしまった結果、修了が1年伸びました。
卒業後はD進せずに就職します。
2021年4月 M1～
この頃は指導教員と1対1のゼミをしていた。当時の肌感覚では（就職とD進どっちがいいかな～）みたいな感じだった。毎週のように論理のガバを指摘されてゼミが炎上する日々を送る。
炎上を繰り返す中で少しずつ精神をすり減らしていき、そのせいで予習もままならないみたいな悪循環を繰り返す。M1の終わりの時点での進度はとてもD進できるようなものではない状況だった。しかし就活は何もしてません。*1
とりあえず就活に軌道修正することにしたのですが、精神的に参っていたので、この時点でもう一年延期するつもりでいました。そして何もかもを放棄して１日中寝込んでました。
2022年4月 M2～
この頃は何もかも情熱を失っていた。研究が楽しくないだけならいいけど、趣味としての数学も楽しくなかった。サークル*2にも足を運べなくなり、競技プログラミングにもOMCにもやる気が出ないというような状況だった。
今だから言うけどこれを質問したの僕です
質問（数学の楽しさが思い出せない）
— 結城浩 / Hiroshi Yuki (@hyuki) 2022年4月21日
私は医療の専門家ではないので、あなたが日常生活に支障をきたすような状態ではないとして回答します。深刻な状態なら、専門家にご相談ください。（続く）#結城浩に聞いてみようhttps://t.co/knwDIxAtnc pic.twitter.com/KFexePCiKg
ただ、義務のようにゼミをこなして炎上を繰り返す無限ループをただただこなすだけのマシーンでした。
就活も義務のようにやってました。インターンに落ちたりインターンに落ちたりインターンに落ちたりした。研究と就活の二重のプレッシャーはとてもしんどいです。
指導教員の言われるままに過ごした結果、2023年の1月（修士論文提出期限より後）のときに指導教員が言うには主結果のようなものが出来上がったらしいです。指導教員から来年前期の半期休学を勧められたので、M3の前期は休学することにしました。
就活 2023年1月～2023年3月
1月にとある会社にエントリーしました。それまでは数ある会社のうちの一つだと思っていたのですが、説明会を聞いてなにか来るものがありました。そのあといろいろな選考作業を得て確信に至り、3月に内定をもらいました。その会社に入社予定です。
内定をもらってからはかなり心が楽になりました。ちなみに自己紹介で「趣味は競技プログラミングです（まあ最近全くやってないけどな！）」と言ったときにレートを褒められた経験は初めてでした。その結果競プロを再開するモチベが湧きました。2023年あたりで一時的に競技プログラミングを再開していろいろやってました。
オンサイト（Toyota Programming Contest 2023 Spring Final）にも行きました。これについては予選を通過できたのは奇跡です（予選の時期が再開したばっかのときだったので）
休学 2023年4月～2023年9月
何をしていたのかと言うと、完全に研究のことをシャットアウトして人生をしていました。
サークルに積極的に足を運びました。OMCのコンテストにも復帰するようになりました。研究活動に関しては何もやっていないような状況でしたが、「以前感じたような数学の楽しさを思い出す」ことはできたと思います。
趣味で物理や化学の勉強にも手を出しました。楽しかったですが研究は何もやってません。
ただ、研究のことを何もやっていないことに対する焦燥感は頭の片隅でずっとありました。
復学～修論提出 2023年10月～2024年2月
復学したときに「あなたはもう修論を書くだけなんだからさっさと書いて卒業してください」と指導教員に言われました。研究に関する負の思い出が蘇ってしんどかったですが、一方で趣味に対する情熱は戻っていたので比較的耐えられました。なんとか重い体を動かして書き切りました。ただ執筆期間中は四六時中発狂してました。
修士論文を提出しました！！！
— しゃかやみ (@shakayami_) 2024年1月18日
修士論文審査合格予定者になってました
— しゃかやみ (@shakayami_) 2024年2月14日
これを書いている時点では確定ではないけど、一応
なぜD進しないことにしたのか
修士課程に進学した場合、将来は大まかに2通りあります。
①D進、つまり博士後期課程に進学 雑な説明をすると研究者の道を志すという感じです
②一般企業に就職 就職する際にも専攻分野を生かした企業に就職できる場合があるし、全く関係ない企業を選んでも構わない
自分は①と②のどちらにするかを決めるのはとても苦心しました。どちらも自分には厳しいと思ったからです。
①を目指すなら研究を今以上に頑張る必要があります。現状研究はあまりうまくいってない＋研究活動（分野）に対してモチベが全くわかないというような状況であり、さらに周りの小中高大の同期の人々が立派に働いているのをSNSで眺める中、親に経済的負担をかけている状況が精神的に耐えられず、それがプレッシャーになって押しつぶされていました。（注：博士後期課程に進学した場合、給料をもらえるどころかむしろ逆で、自分（の親）が学費を払う必要があります。また、優秀な場合は学振によってお金が貰える場合があります。）
結局、金を払ってしんどい思いをするのと、金をもらってしんどい思いをするのだったら、（片方の「しんどさ」がよほど天元突破しない限り）金をもらうほうがまだマシだと思ったため、②の就職に軌道修正をしました。そのことを決めた時点では23卒での就職はほぼ手遅れでした。
ネットにはこのような書き込みもあります。
引用出典
自分はまだ社会人としての経験がないので真偽はわからないのですが、大学院から就職したFF2名もこれに同意していました。
プロセカ
大学院生活では、プロセカ（プロジェクトセカイ カラフルステージ feat. 初音ミク）にはまっていました。プロセカは大学院生活の心の癒やしでした。研究活動がとてもしんどかったけど、自分も宵崎奏が作った曲に救われたのかもしれない。また、研究活動で精神が疲弊した結果家がゴミ屋敷になりましたが、残念ながら家事代行の望月穂波さんはいません。悲しいね ちなみにKUMAFにも入会しました
大学院時代好きだったアニメ
ぼっち・ざ・ろっく！（2022年秋クール） もともと原作を知ってて持ってたので流れで見た。
コマの間にある何気なく面白いギャグが映像化された結果超面白くなってたことに感動～！！後藤さんギター上手いのね～！！
原作に対する興味も再燃して何度も何度も読み返しました。読み返すたびに新しい発見があってとても楽しかったです。
アニメは神だった（ちなみに聖地にも行ったよ）
サークル
作問サークルです。Lim_Rim_ 等とともに創設時からいろいろやってました。学部含めて京都での生活の殆どをここ過ごしたためこのサークルに対して思い入れがありすぎる。
2023年においてはいろいろしてましたが、例えばNF杯2023の企画準備をしていたうちの一人が自分です。
研究者の道は諦めるの？
「社会人博士をやりたい！」とはさすがに言えない。修論でここまで疲弊していたので破滅する未来しか見えない。
この先どうなるかはわからないけど、やっぱり数学は楽しいから趣味としてやっていきたいと思う。せっかく楽しい気持ちを思い出せたので忘れずにいたい
これからの当分の目標
地盤を固める それは
仕事においても
学問においても
趣味においても
日常生活においても
人間関係においても
さらに持続可能な社会人生活を目指す
長距離走だと思って程々に（健康を維持できる範囲で）頑張ろうと思います。
競技プログラミングについて
復帰するためにちまちま過去問解いているけど「これが〇〇diffってマジ？インフレしすぎだろ」って無限回思っているので恐ろしいばかりです。今コンテスト出たら無限にレートが下がる気しかしません。むしろ玉砕覚悟で積極的に出たほうがいいのかもしれないとも思いました。
研究内容って何やってたの
M1のはじめからカラザスシュレーブを読みながら論破されることを何回も繰り返す
満身創痍になりながら論文を読む （指導教員が）なんやかんやすると主結果ができあがる ごめんなさい僕よりも指導教員のほうが詳しく知ってると思います。
最後に これから起こることを何も知らない人の図
【報告】
— しゃかやみ (@shakayami_) 2020年9月11日
京都大学大学院理学研究科の数学先端コースに合格しました
↑1年後には（なんで自分受かったんだろう？採点ミスかな？）ってずっと思ってるよ
— しゃかやみ (@shakayami_) 2021年4月7日
↑スーツに着替えたけど直前で行くのがめんどくなってオンラインにした。なのでクライアントがtwitter Web Appになっている
勉強しない=留年, 勉強=留年しない
概要
勉強＋勉強しない=留年+留年しない
(1+しない)勉強=(1+しない)留年
勉強=留年
だったら遊ぼっか
考察
Rを可換環とする。Rの元a,b,cについて
勉強=a,留年=b,しない=cとおくと、
$$ac=b$$
$$a=bc$$
が成立している。このとき、$a=b$となるだろうか？
まず、「(1+しない)勉強=(1+しない)留年」まではどのような可換環でも成り立つ。これは環の公理として分配法則が課されているからである。
しかし、その次の行で両辺を(1+しない)で割っているが、そこが怪しいのである。
真っ当な例としては、(1+しない)=0であるような場合である。御存知の通り両辺を0で割ることはできない。つまり、勉強と留年が加法の逆元の関係にあって、しない=-1であるような場合がすぐ思いつくような反例である。
では、すぐに思いつかないような反例とはなんだろうか？
そもそも、両辺を(1+しない)で割るとはどういうことなのかを詳細に書き直してみると、
(1+しない)勉強=(1+しない)留年より、(1+しない)(勉強-留年)=0
$$(1+c)a=(1+c)b\Rightarrow (1+c)(a-b)=0$$
という式があって、ここで、$1+c\neq 0$ならば、$a-b=0$が従うということを言っている。
つまり、「$\forall x,y\in R,xy=0\Rightarrow x=0\lor y=0$」ということである。
この性質は全ての環で成り立つとは限らない。ここで、このような性質が成り立つような環のことを整域という。とりあえず、$R$が整域のときの解を全列挙してみる。
まず言えることとして、
$$ac=b\Rightarrow ac^2=bc=a$$
$$bc=a\Rightarrow bc^2=ac=b$$
$a=0$ならば、$ac=0$より、$b=0$である。このとき、$c$はどんな値でも構わない。よって、$(a,b,c)=(0,0,c)$が解である。
$a\neq 0$ならば、$c^2=1$より、$(c+1)(c-1)=0$である。整域の性質より、$c+1=0$または$c-1=0$である。よって、$(a,b,c)=(a,-a,\pm 1)$が解である。
よって、$R$が整域であるときの解は(勉強,留年,しない)=(0,0,x),(x,-x,1),(x,-x,-1)が全てである。
この中で勉強=留年が成り立つならば、 勉強=留年=0 または しない=1 となる。
前者は勉強も留年も全て虚無であることを言っていて、後者は否定が否定でなくなってるので、どっちも感覚的におかしい。
感覚的には「しない=-1」であるが、この場合は(1+しない)=0であり、0で割ってしまっているのでおかしいし、勉強=留年=0でない限り勉強=留年とはならない。
数学的に正しくてかつ感覚的にも合致している解は存在するだろうか？
一般の環で$ac=b,bc=a,a=b\neq 0,c\neq 1$となるような状況を考えてみる。
このとき、$ac=a$より、$a(c-1)=0$である。よって、$R$が整域でなければ可能性はある。というか、整域でなければ解はある。
例えば、$\varepsilon$を、$\varepsilon^2=0,\varepsilon\neq 0$となるような数とする。より踏み込んだ話をすると、$\varepsilon$は$\mathbb{R}[x]/(x^2)$において、$\varepsilon=[x]$である。
このとき、$\varepsilon^2=0,\varepsilon\neq 0$で$(a,b,c)=(\varepsilon,\varepsilon,1+\varepsilon)$が解となる。
他にも、$R=\mathbb{Z}/6\mathbb{Z}$としたときの$(a,b,c)=(2,2,4)$も解である。
まあ、どのような例であれ、解が存在したからといってこの「証明」が数学的に正しいわけではない。上記でやったことは勉強=留年となるような例を列挙したことであって、勉強=留年が成り立つことを証明したわけではない。というか、勉強≠留年となるような例のほうが遥かに多いだろう。
おわりに
残念ながら、この議論は数学的には正しくない。正当化しようと頑張ったけど厳しかった。やはり(1+しない)で割っているところのギャップを埋めるのは難しい。
また、こうやってどうでもいいことばっか考えて時間を無駄にしてしまったので、残念ながら留年してしまいました。これこそ勉強しない=留年かな
熱効率を計算するプログラム
突然ですが問題
熱効率はいくつ？
あ、言い忘れてましたが、以降この記事では全て単原子分子理想気体とします
これはまあ基本問題です
この手の問題は表を作るのが良いでしょう
| 経路 | dU | Q | W |
| A→B | $\dfrac{3}{2} P_0V_0$ | $\dfrac{3}{2} P_0V_0$ | $0$ |
| B→C | $3 P_0V_0$ | $5 P_0V_0$ | $-2P_0V_0$ |
| C→D | $-3 P_0V_0$ | $-3 P_0V_0$ | $0$ |
| D→A | $-\dfrac{3}{2} P_0V_0$ | $-\dfrac{5}{2} P_0V_0$ | $-P_0V_0$ |
Qの列を見て、符号がプラスのものとマイナスのものに分ける
A→BとB→Cがプラスで、C→DとD→Aがマイナスである。
で、符号がプラスのものがエネルギーの入力、符号がマイナスのものがエネルギーの出力となる。
で、入力は$\dfrac{13}{2}P_0V_0$で、出力は$\dfrac{11}{2}P_0V_0$です。入力されたエネルギーにおいて、一部分は仕事をしますが残りは出力エネルギーとなる。
エンジンをイメージしてほしい。このようなエンジンがあったとき、最初に$\dfrac{13}{2}P_0V_0$の分だけのエネルギーが投入さるが、そのうちエンジンがする仕事は$\dfrac{13}{2}P_0V_0-\dfrac{11}{2}P_0V_0=P_0V_0$であり、残りの$\dfrac{11}{2}P_0V_0$はただエンジンが熱くなったりするだけで仕事をせずに無駄になるエネルギーになると思っておこう。
すると、熱効率は
$$1-\dfrac{\dfrac{11}{2}P_0V_0}{\dfrac{13}{2}P_0V_0}=\dfrac{2}{13}$$
となる。
次の問題にしようと思ってたものがむずいのでもうちょっと良心的なものを置く
断熱変化では$PV^\gamma,\gamma=\dfrac{5}{3}$が一定なので、$8^{5/3}=32$よりポアソンの式は満たしている。
これも表を書く
| 経路 | dU | Q | W |
| A→B | $\dfrac{93}{2} P_0V_0$ | $\dfrac{93}{2} P_0V_0$ | $0$ |
| B→C | $-36P_0V_0$ | $0$ | $-36P_0V_0$ |
| C→A | $-\dfrac{21}{2}P_0V_0$ | $-\dfrac{35}{2} P_0V_0$ | $7P_0V_0$ |
入力は$\dfrac{93}{2}P_0V_0$で、出力は$\dfrac{35}{2}P_0V_0$なので、
熱効率は
$$1-\dfrac{\dfrac{35}{2}P_0V_0}{\dfrac{93}{2}P_0V_0}=\dfrac{58}{93}$$
ということで次
C→Aは、PV図で斜めの直線となっている。つまりこれは定積変化でも定圧変化でも等温変化でも断熱変化でもない。
仕事の部分は、PV図の面積を求めればOK（つまり積分する）、内部エネルギーの変化は温度の変化だけ見ればOKなので、Qはその差を求めればOKなのでこう書けば良さそう？？？
| 経路 | dU | Q | W |
| A→B | $-\dfrac{3}{2} P_0V_0$ | $-\dfrac{5}{2} P_0V_0$ | $P_0V_0$ |
| B→C | $\dfrac{3}{2}P_0V_0$ | $\dfrac{3}{2} P_0V_0$ | $P_0V_0$ |
| C→A | $0$ | $\dfrac{3}{2} P_0V_0$ | $-\dfrac{3}{2}P_0V_0$ |
なので熱効率は
$$1-\dfrac{\dfrac{5}{2}P_0V_0}{\dfrac{3}{2}P_0V_0+\dfrac{3}{2}P_0V_0}=\dfrac{1}{6}$$
…としたいところだけど、残念ながらこれは間違っている。
結論から言うと、正しい表はこれだ！
| 経路 | dU | Q | W |
| A→B | $-\dfrac{3}{2} P_0V_0$ | $-\dfrac{5}{2} P_0V_0$ | $P_0V_0$ |
| B→C | $\dfrac{3}{2} P_0V_0$ | $\dfrac{3}{2} P_0V_0$ | $0$ |
| C→D | $\dfrac{21}{128} P_0V_0$ | $\dfrac{49}{32} P_0V_0$ | $-\dfrac{175}{128}P_0V_0$ |
| D→A | $-\dfrac{21}{128} P_0V_0$ | $-\dfrac{1}{32} P_0V_0$ | $-\dfrac{17}{128}P_0V_0$ |
最初の図も訂正しておこう。問題文の図もこうした方がいい
ということで正しい答えは
$$1-\dfrac{\dfrac{5}{2}P_0V_0+\dfrac{1}{32}P_0V_0}{\dfrac{3}{2}P_0V_0+\dfrac{49}{32}P_0V_0}=\dfrac{16}{97}$$
そう、新しい点Dを置かないとだめなのである！
なぜこうなるかというと、C→Aの経路をたどる途中で、最初はエネルギーが注入されるけどそれはDまでで、Dを通り過ぎた瞬間エネルギーが注入から放出に切り替わるのである！つまり、熱効率を変化するためにはδQの符号を追跡しなくてはいけないけど、この場合はδQの符号が途中で変わることを考慮しなくてはいけないのである！
δQの符号が途中で変わること、は定圧変化でも定積変化でも等温変化でも断熱変化でも起こり得ないので、このような特殊な変な経路をたどるときに初めて考慮する必要が出てくるのである。
で、気になるのがどうして途中で切り替わるのか、切り替わるとしてなぜ$\dfrac{9}{8}P_0,\dfrac{15}{8}V_0$だとわかるのかという問題である。
一般論として、このような熱機関において、各パラメータは変数で置くことができる。
内部エネルギー$U$は$(P,V)$の関数で以下のようにかける
$$U=\dfrac{3}{2}PV$$
なので、$U$の微小変化は以下のように書ける
$$dU=\dfrac{3}{2}\{(P+dP)(V+dV)-PV\}$$
$$=\dfrac{3}{2}(PdV+VdP)$$
（微小量×微小量は無視できるので$dPdV=0$である）
で、
仕事$\delta W$は以下のように書ける
$$\delta W=-PdV$$
すると、熱力学第一法則より、
$$\delta Q=\dfrac{3}{2}VdP+\dfrac{5}{2}PdV$$
となる。
なぜ$U$の微小変化は$dU$なのに$Q,W$の微小変化は$\delta Q,\delta W$と書いているかというと、$\dfrac{3}{2}(PdV+VdP)=f(P+dP,V+dV)-f(P,V)$となるような関数$f$は存在する$f(P,V)=\dfrac{3}{2}PV$とおけばいい
けど、$-PdV=g(P+dP,V+dV)-g(P,V)$なる関数$g$や$\dfrac{3}{2}VdP+\dfrac{5}{2}PdV=h(P+dP,V+dV)-h(P,V)$となる関数$h$は存在しないのである！
これは、$U$は状態量であるが、$Q$や$W$は状態量じゃないからこうなってる
状態量とはどういうことなのか？という人のために説明
上の表とかを書くときに、$U$を計算するときは始点と終点の情報だけわかってれば求めることができる。正直言って、始点と終点さえ同じだったら、途中の経路がどのようなものであっても内部エネルギーの変化は同じなのである。
しかし$Q$や$W$はそうではない。$Q$や$W$を計算するときは、最終的な答えが途中の経路に依存するのである。なので、始点と終点の情報だけでは計算できない。途中の経路がどのようなものだったのかという情報が必要である。
で、最終的にQやWの計算については$\delta Q$や$\delta W$を線積分すれば求めることができる。
で、線積分だけど、$(P,V)=(f(t),g(t))$というような媒介変数で書ける経路において$a(P,V)dP+b(P,V)dV$を線積分したいなら
$$\oint a(P,V)dP+b(P,V)dV=\int a(f(t),g(t))f'(t)dt+\int b(f(t),g(t))g'(t)dt$$
というようになる。
本題に戻る。このようなC→Aの直線経路において、
$$(P,V)=((2-t)P_0,(1+t)V_0)$$
というような媒介変数で書くことができる。ただし$t$の動く範囲は$0\leq t\leq 1$
で
$$\delta Q=\dfrac{3}{2}VdP+\dfrac{5}{2}PdV$$
$$=\dfrac{3}{2}(1+t)V_0 \cdot (-P_0)dt+\dfrac{5}{2}(2-t)P_0 \cdot V_0 dt$$
$$=\left(\dfrac{7}{2}-4t\right)P_0V_0dt$$
となっている。
で、tごとに$\delta Q$の微小変化を見ると、
$0\leq t\leq\frac{7}{8}$のときに$\delta Q\geq 0$
$\frac{7}{8}\leq t\leq 1$のときに$\delta Q\leq 0$
となる。なので、$t=7/8$となる地点、つまり$(P,V)=(\dfrac{9}{8}P_0,\dfrac{15}{8}V_0)$で一旦分けないといけないのである。
これを踏まえた上で次の問題
いや、さっきの問題でやることはわかったけどただクソめんどいだけじゃん
ということなので
退屈なことはPythonにやらせよう
ということでソースコード、ペタッ！ｗ
gistb858bb113423b471eeaa29a8bd22622c
説明
PV図上の点において、$N$個の点からなるサイクルを考える、各点の間の経路は全部直線であると仮定した場合、熱効率はいくらになるか？
この記事を読んだ人々が真似しやすいように仕組みも書きます。
まずは直線経路上において受け取った熱の量と放出した熱の量を計算する方法から
$a,b,c,d$を正の定数とします。（変数のdと微小量のdでダブってるので以降微小量は$\Delta$で書きます）で、$(aP_0,bV_0)\to (cP_0,dV_0)$に向かう直線の経路を考えたとき、
$$P=((c-a)t+a)P_0,V=((d-b)t+b)V_0$$
となります。
で、このとき、
$$\delta Q=\dfrac{3}{2}V\Delta P+\dfrac{5}{2}P\Delta V$$
$$=4(c-a)(d-b)t+\dfrac{3}{2}b(c-a)+\dfrac{5}{2}a(d-b):=At+B$$
とします。
$0\leq t\leq 1$において、$At+B\geq 0$ならば熱を受け取っていて、$At+B\leq 0$ならば熱を放出しています。なので、$0\leq t\leq 1$の範囲内で$At+B$の符号が変化するかどうかを確かめます。符号が変化するなら符号の変化点で区切ります。符号が変化しないならば、
$$U=\dfrac{3}{2}(cd-ab)P_0V_0$$
と、
$$\Delta W=(d-b)((c-a)t+a)P_0V_0dt$$
で、これをtについて0から1まで積分すればOK
こうすることで、直線経路上において、（受け取った熱の量、放出した熱の量）の組を計算することができます
次に、熱効率について
これは全ての線分上において、受け取った熱の量の合計$O_{in}$と放出した熱の量の合計$Q_{out}$を合計して、それについて$$1-\dfrac{Q_{out}}{Q_{in}}$$とすればOK
で、このプログラムは、$Q_{out}\gt Q_{in}$のときは熱効率が計算しないようにしている。これを判定するために仕事を計算している。$\oint_C PdV\lt 0$なら熱効率は計算できない。これは$PV$図において時計回りの経路なら熱効率が計算できるけど、反時計回りの経路ならできないということである。
で、質問の答え（八角形の経路）としては、プログラムに以下の入力を打ち込むだけ
print(thermal_efficiency([(2,1),(3,1),(4,2),(4,3),(3,4),(2,4),(1,3),(1,2)] ) )
というわけで答えは32/119
よくある質問
なんで断熱変化や等温変化に対応してないのですか？
答えが有理数にならないから大変そうだと思った。
とりあえず等温変化について
等温変化だと$P=tP_0,V=\dfrac{V_0}{t}$と書くことができる。$\alpha \leq t\leq \beta,0\lt \alpha \lt \beta$
$$dP=P_0dt,V_0=-\dfrac{V_0}{t^2}dt$$
なので、
$$\dfrac{3}{2}VdP+\dfrac{5}{2}PdV=\dfrac{3}{2}\cdot \dfrac{1}{t}-\dfrac{5}{2}\cdot \dfrac{1}{t}P_0V_0dt=-\dfrac{1}{t}P_0V_0dt$$
なので、これを積分すると自然対数が出てくる。
断熱変化についても、$\delta Q=0$なので対処しやすそうに見えるけど、$PV^{\gamma}=const$なので始点終点によってはパラメータに三乗根が出てくる。
これらに対してどうにかするには厳密な値を諦めてfloatで近似値を出す実装にするか、伝家の宝刀sympyを使うかくらいしかなさそう。そしてプログラムのインプットが経路の頂点だけになってるのまずそう。各経路がどのような変化かを明言する必要がありそう。とりあえず直線変化（∋定圧変化、定積変化）、等温変化、断熱変化だけに対応すれば良さそう？実装めんどいので妥協
δA=f(P,V)dP+g(P,V)dVみたいなのが状態量であるかどうかってどうやって判定すればいいですか？
これは外微分をすればOK
というわけでこの「微小量みたいな形になっているもの」さらに形式的に微分するみたいなことをする
$$d\delta A=\{\dfrac{\partial f}{\partial P} (P,V)dP+\dfrac{\partial f}{\partial V} (P,V)dV\}\land dP+\{\dfrac{\partial g}{\partial P} (P,V)dP+\dfrac{\partial g}{\partial V} (P,V)dV\}\land dV$$
$$=\dfrac{\partial f}{\partial P}dP\land dP+\dfrac{\partial f}{\partial V}dV\land dP+\dfrac{\partial g}{\partial P}dP\land dV+\dfrac{\partial g}{\partial V}dV\land dV$$
で、微小量と微小量に対して$dx\land dy$になってるのは何やねんとなるのだが、
とりあえず以下のような計算法則が成り立つものだと思っておけばOK
$$dx\land dy=-dy\land dx$$
$$dx\land (bdy+cdz)=b dx\land dy+c dx\land dz$$
$$(a dx+b dy)\land dz=a dx\land dz+b dy\land dz$$
ということでかけ算の順序を入れ替えると符号が逆になることに注意。「ベクトルの外積みたいなもの」だと思えば理解できる人がいるかも
というわけで計算練習をすると、先程の計算規則に対して$x=y$とおくと
$$dx\land dx=-dx\land dx$$
なので$$dx\land dx=0$$
となる。
詳しく知りたい人へ→
ということで、
$$d\delta Q=\{\dfrac{\partial f}{\partial V}-\dfrac{\partial g}{\partial P}\}dV\land dP$$
である。これが0にならなければ、確実に存在しない。
つまり、
$$Q=h(P,V)$$ならば
$$\delta Q=\dfrac{\partial h}{\partial P}dP+\dfrac{\partial h}{\partial V}dV$$
なので、
$$d \delta Q=\{\dfrac{\partial^2 h}{\partial P\partial V}-\dfrac{\partial^2 h}{\partial V\partial P} \}dV\land dP$$
であり、お行儀が良い関数ならば偏微分する順番を入れ替えても同じ結果になるのでこれが0になるのである。
つまり、もう一回微分して0になることが状態量が存在することの必要条件である。
一方、もしこれが0になったら、これは状態量である。$f$を$P$で積分したり$g$を$V$で積分したりすると候補が見つかるかも
δQは状態量にはならないけどδQ/Tは状態量になるでは？と思いましたがどうなんですか
おっいい質問ですね
$$\delta Q=\dfrac{3}{2}VdP+\dfrac{5}{2}PdV$$
で
$$\dfrac{\delta Q}{T}=\dfrac{3}{2}\dfrac{V}{T}dP+\dfrac{5}{2}\dfrac{P}{T}dV$$
で、$PV=nRT$より、
$$\dfrac{\delta Q}{T}=\dfrac{3}{2} nR\dfrac{dP}{P}+\dfrac{5}{2}nR \dfrac{dV}{V}$$
で、
$$d\dfrac{\delta Q}{T}=0$$
なので状態量である。
で、
$$S=\dfrac{3}{2}nR \log\{PV^{\gamma}\}$$
という量を置くと（$\gamma$は比熱比で単原子分子理想気体ならば$\gamma=5/3$）
$$dS=\dfrac{\delta Q}{T}$$
となります。
このSには名前がついていて、エントロピーというらしいですね
$\delta Q=0$なら$dS=0$なので、断熱変化のときに変化しない量となります。
知らんけど （自分はこのような理解をしているのですが、間違ってたらこの記事を燃やしてください）
chatGPTの数学力ってどうなの？わざわざ課金して試してみた結果…
導入
というわけでchatGPTの数学力を試してみたいと思います
GPT-4やWolframみたいなプラグイン機能があるので課金して試してみることにした
調査日：2023年5月・6月
- 導入
- GPT-3.5だとどうなの？
- GPT-4&プラグインだとどうなる？
- Wolfram Alphaができることはできるっぽい
- Wolframでできることは実は数学だけではない
- chatGPTの限界を探る
- Wolfram Alphaでも解いてくれない場合は厳しそう
- Wolfram Alphaが答えてくれない場合は適当に間違ったことを言う可能性がある
- Wolfram Alpha could not understandでも正答してくれる場合も一応ある
- 効率的なアルゴリズムで計算してくれるとは限らない
- Wolfram Alphaのリンクを貼られるけどプロンプトでは答えてくれないパターンがある
- AIによる立式が間違っているせいでWolfram Alpha could not understandじゃなくても間違えてる可能性がある
- 英語で質問したほうがうまくいきそう？
- ゴリ押しでAIをわからせれば解いてくれる場合もある
- 無理なものは無理である
- perplexity AIとの比較
- 証明系で試してみる（あんまりWolfram関係ない）
- 大学入試問題を解かせる
- その他
- まとめ
- FAQ
GPT-3.5だとどうなの？
ゴミじゃん
というわけで課金します
ちなみにこの記事は以降はもう3.5は出てきません。あとはずっとGPT4でプラグインはWolfram・Web Pilot・Show Meの三本立てでお送りします
GPT-4&プラグインだとどうなる？
良さそう、やっぱGPT-4は神やな！みんなも課金しよう！課金最高！
...これでは終わりません
というわけでもっと検証を重ねることにしました。
結論から言うと、このWolframというプラグインやGPT-4はどうなのか？というと
良くも悪くも、Wolfram Alphaができること「は」できる。
Wolfram Alphaではできなかった場合の結果は不定です。
結局、構造としては基本としてはGPT-4がWolfram Alphaに丸投げしている。そのように見えます。
そうなると、Wolfram AlphaだけでいいしchatGPTいらないじゃんってなりますが、まあ、Wolfram Alphaのコマンドを調べる手間が省けて直感的な日本語の指示で計算してくれるのは良いのかもしれない？とも思いました。
また、GPT-4かつプラグインありでも間違える可能性は十分にあります。
というわけで、AIとの格闘の記録を見ていきましょう！
Wolfram Alphaができることはできるっぽい
僕は高校数学の美しい物語の信者なので、この記事を参考に進めていきたいと思います。
進数表記
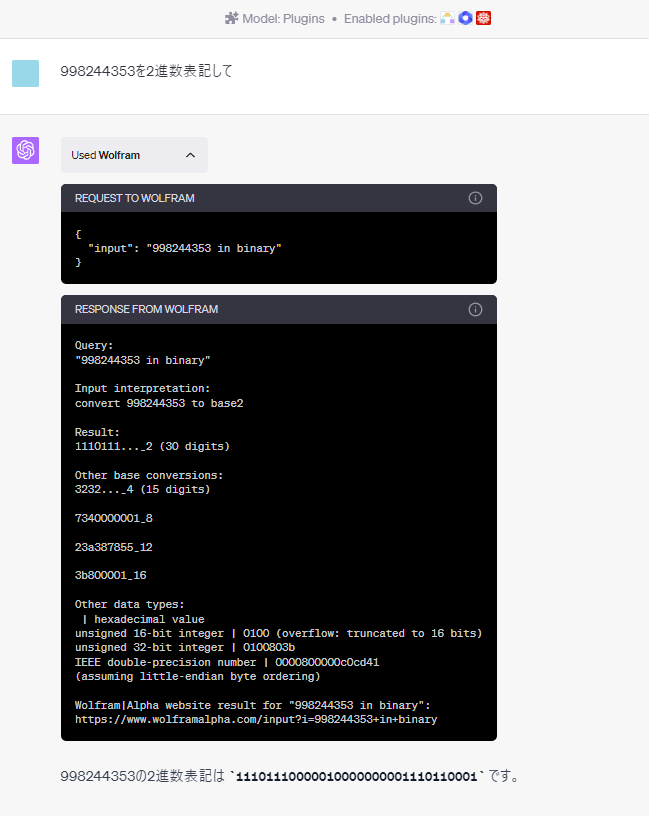
危なっかしいけど一応クリア（注：998244353は競技プログラミングで有名な素数で、1+119×2^23であることが知られているので、0が連続しなければおかしいとわかる）
式の展開
一応合ってそう（ただa^3(-b^2)という表記がキモい）
式の因数分解
合ってる
関数のグラフ
たぶんこんな感じであってそう
分母の有理化
合ってるかは知りません
ただ、Wolfram Alphaに投げた結果と同じだったことは言っておきます
複素数
合ってる
部分分数分解
合ってそう
領域の図示
合ってる
代数方程式の厳密解・連立方程式
合ってる
漸化式
nが非常に大きい場合にのみ近似的…？つねに厳密に正しくなるはずだが？
まあ合ってるけど、一応他のも投げる
なんで解かんねん
ちなみにWolfram Alphaは計算してくれた
一番上のa(1)=1,a(n+1)=a(n)+sqrt(1+a(n)^2)はWolfram Alphaでも無理だった。
証明は読者への演習問題とします。
難易度を下げても解いてくれなかった
一方Wolfram Alphaは余裕で計算してくれた
シグマ計算
合ってる。TeXの表記が若干キモいけど許容範囲内
極限計算
合ってそう
微分計算
合ってる。3回微分してもとに戻るのがミソ
不定積分
合ってそう。想定解はlog(x+1/2+sqrt(x^2+x+1))だけど、logの中身が(2/sqrt(3))倍されている→結果として定数分だけずれているだけなので問題なし
定積分
残念
ちなみにWolfram Alphaくんは解いてくれた
さすがにむずいのでもっと簡単なやつを投げる
合ってる
流石に積分は調査対象の範囲がでかすぎるので詳しいことはまたの機会に
偏微分
まあ良さそう
テイラー展開
合ってる
係数はフィボナッチ数列になります
行列式
合ってそう
逆行列
合ってる
固有値と固有ベクトル
まあ良さそう
期待値
Wolframでできることは実は数学だけではない
そもそもWolfram Alphaでできることは数学以外にも色々あるので、試してみましょう。じゃあWolfram Alphaだけでええやんけとも思うけど、日本語でコマンド送れるというのはアドなのかも？知らんけど
また、ここで挙げたもの以外でもWolfram Alphaでできることは多いので試してみるのも良いのかもしれない。
天文
注意：このプロンプトの検証日は2023年5月31日
化学
生物
地理
問題を分割して複数のコマンドを送った結果の情報を処理しているのえらい
歴史
日時を聞くくらいならなんとかなりそう。ガチの論述に対処できるかは未検証なので不明
chatGPTの限界を探る
これを課題を解くのに使えるか？と思ったが結論から言うと非推奨です。Wolfram Alphaを課題に使うのは問題ないと思いますがchatGPTを使うのはやめておいたほうが無難です。
Wolfram Alphaでも解いてくれない場合は厳しそう
自作問題をいくつか解かせてみた。ただしこれらの問題はWolfram Alphaでは解いてくれませんでした。
だめっぽい
次
お前が専門家になるんだよ！
次
chatGPT、お前と戦いたかった…！
次
だめでした
Wolfram Alphaが答えてくれない場合は適当に間違ったことを言う可能性がある
先駆者兄貴の調査によると、約1.01%なのでchatGPTが間違っています。
ちなみにこれはWolfram Alpha could not understandのパターンなのでchatGPTが憶測で解答しています。
また、これをツイートしたら天文学に詳しいフォロワーから「直感的に7%もあるわけない」というリプが来ました。
Wolfram Alpha could not understandでも正答してくれる場合も一応ある
合ってそう
これに関してはWolfram Alphaではできなかったっぽい
結局、Wolfram Alphaでできなかった場合の結果は不定形なので、出力を人間が検証する必要が出てきます。
効率的なアルゴリズムで計算してくれるとは限らない
Wolfram Alphaのリンクを貼られるけどプロンプトでは答えてくれないパターンがある
リンクを見れば答えが書いてあるパターン
AIによる立式が間違っているせいでWolfram Alpha could not understandじゃなくても間違えてる可能性がある
解いてくれなかったパターン
出典：OMC057(D)
以下省略
ダメみたいですね…
一方、人間が適切にプロンプトを送れば正答できる場合もあります。
途中ですこしぐだってますがまあ良さそうです。
結局この問題をAIに正解させるためには人間側がRavi変換を知っている必要がありそうです。
英語で質問したほうがうまくいきそう？
解いてくれなかった
英語で質問したらこうなったけど、どうして
ゴリ押しでAIをわからせれば解いてくれる場合もある
$$\lim_{n\to\infty}\dfrac{1}{n^3}\sum_{1\leq a,b,c,\leq n}\mathrm{gcd}(a,b,c)$$
出典は自作です。Wolfram Alphaでは解いてくれませんでした。
長い道のりだった…
無理なものは無理である
出典：OMC057(F)
道のりは長そうです…またAIをわからせるのは大変そうなのでさじを投げました。
perplexity AIとの比較
できなかった
一方perplexity AIだとこうなる
Perplexity AIは検証のしがいがありそうではある
証明系で試してみる（あんまりWolfram関係ない）
筆者が解析系なので代数や幾何の質問あんまりないの許して
合ってそう（対偶法なの？とは思う）
良さそう
さすがに定番なやつは対策済みか
うーん
図を書くのは無理そう？（show Meというプラグインを入れた上でこうなってる）
次
det(A)=±1⇒逆行列の係数は整数は合ってるけど、その逆の証明が間違い
というか証明になってない（な～にが「保証はありません」や）
しかし、指摘したら一発で当ててきた
次
「群が全ての部分群に対してアーベルであるとき、その群自身もアーベル群であるという定理」そんな定理初めて聞いたが…？まあ全体群もアーベルだったら明らかなので全ての「真」部分群だと思うけど… あっ反例あるやんけ（3次対称群S_3など）
うまい具合にはぐらかされた気がする…
証明系はファクトチェックするのがめんどい たぶん中心が単位元じゃないところの証明がおかしい
うーん
こんだけ自信満々に書かれると逆にこっちが自信がなくなってしまう…
この証明は間違ってますよね…？というかメチャクチャすぎてどこから指摘すれば良いのかわからんけど ああ頭がおかしくなりそう
おっ、さっきよりはまともなこと言ってそう（細かい部分のガバを確認する気力は無くなりました）
ん？急にどうした
ど う し て
もう無理そうなので以下省略
というか何度も何度も怪文書を送られてくると実は合っていて自分が間違っているのでは？という錯覚にに陥ってしまう
わざわざTwitterでアンケートを取ってしまった
アンケート
— しゃかやみ (@shakayami_) 2023年5月29日
次
トポロジカルコーム…知らない言葉だ ググっても出てこなかった
…と思ったけど英語でググったら出てきた
また、以降の対話は英語でググる前にしたものです
少し考えてみたけど、たぶんこれはだいたいあってそう
まず(0,0)から(1,0)へのパスはないので弧状連結じゃない
連結であるためには開集合2つに分離する必要がある
で、(1,0)の一点集合で分離するしか無さそうに見えるけど、実際{(1,0)}は開集合じゃない（無限に近い近傍の点が取れるから）ので連結なはず…？
トポロジカルコーム、topological combのことみたいですね…
combとは日本語で櫛（くし）のことみたいです。
群論で脳破壊されたので細かいところのガバを検証する気力はなくなりました…
次
説明が意味不明だったので聞き方が悪かったのかな？と思って同じ質問を2度してしまった
これもダメそうなパターンかな？と思っていたが…
これは正解ですね（AIくんローラー作戦でもしてる？？？）
群論の節で脳破壊されたけど、今回は順当に正答してくれたので安心しました。
次
間違っているとは断言できないけど、こんな表記で大丈夫か？
次
フビニの定理ってこんな簡単に示せたっけ
あくまでこれは証明のだいたいの流れであって証明ではないですね
なんか詳細は見事にはぐらかされました。
次
g(x)=x+f(x)だとS^2からS^2の関数になってないので多分ダメそう
次
これは合ってそう。あえて存在しないものに対して挙げてくださいって言う意地悪な質問をしたけどちゃんと対処してくれた。
次
これは多分良さそう
次
これは合ってそう
次
これは合ってないパターン
次
まあ合ってそう
次
これにLU分解持ってきて大丈夫なの？LU分解のことは知らないけど循環論法の匂いがする
うーん 真偽不明なので保留
次
あえて意地悪な質問をしたけどちゃんと対処してくれた（主張そのものが間違っているので、「証明」をしていたらそれは無条件で間違っているとわかる）
次
これは証明ではないですね
連分数か～
連分数が無限に続けば無理数だと言えますが、そもそもeの連分数は何故この様な形で書けるのでしょうか？
完全に理解したいのだが？
連分数がこうなる理由については教えてくれませんでした。いかがでしたか？
証明関連は検証することが多そうですね
あと、こういう微妙に合ってるか間違ってるかよくわからんやつが大量に送られてくるので気が狂いそう。かといってすべて間違っているわけでもないし、変な記述も多いし、全く自明じゃないことを自明で済ましたりと怪レい行動が多い。
AI生成されたレポートを採点するのは大変そうだと思いました。
大学入試問題を解かせる
まずは2016年の京大
ガバガバ
証明系は信用しないほうが良さそうです
次はどこかの大学
まあ、ありがちな問題なのでどこかで出てると思います。知らんけど
この問題はベタなのですでに誰か解いているだろうな～という思いでググると、すでに解いている先駆者兄貴がいることがわかります。
先駆者兄貴の解説によると、1つめは16-8√2≒4.86になるみたいです。
また、2つめは16/3になります。AIの答えは先駆者兄貴の答えと一致しているみたいです。
答えに円周率が出てこず代数的数になるのが面白いですね
今回のAIくんは比較的まともな返答でした。
次
これもそこらへんで出まくってるので出典はありません
壊れちゃった…
ダメみたいですね…答えは
を参照
訓練された人ならπ/(30√2)だと答えを覚えているはずです。
その他
まあWolfram Alphaでできることはできると思えばOK
次
たまにWolfram関係なしに正答するのはすごい
まあベタな話題ならなんとかなるのだろうか？
次
こういうのに対して、ファクトチェックをWolfram Alphaに頼って問題ないのか？みたいな考えに陥ることはありがち まあWikipediaに書いてある値とは一致してた
次
おっ合ってそう…と思ったけどよく見てみると
オイラー線の定義が「重心、外心、内心を通る直線」と言っていますがこれは間違いです。正しくは「重心、外心、垂心を通る直線」です。
また、九点円の中心は外心と垂心の中点であって、外心と重心の中点ではないはずです。
他にも細かいところがおかしい。
そのことをAIに言いました。
すると…
さっきまで正しかったところを間違った情報に訂正したりしがち（例：外心についての説明など）あと垂心の定義もちがう
あと、フイッター円という名前は初めて聞きました…ググっても英語でググってもTwitterで検索しても出てきません…
次
なるほど帰納法ね…って思ったけどよく見たら途中式ガバガバじゃない？
次
こんなに少なかったっけ？？って思って計算し直したら答えは29C19なので、20030010らしい。普通に間違ってた。じゃあWolframにおくっているプロンプトは何だ？
次
式すら合ってないのでは？大丈夫なのだろうか
GPTがWolframに投げているコマンドがそもそも間違っているっぽい。偏差値を計算するには2乗モーメントを求める必要がある。そもそも偏差値という概念が日本特有のものっぽいので厳しそう？
次
まあ良さそう
他にも検証したいことは多いけどこのままじゃ書ききれないので終わります
まとめ
chatGPTの内容を盲目的に信用するのはやめましょう！それはたとえGPT-4やプラグインを使っていたとしてもです。正解することもありますがやっぱり危なっかしいです。指摘すれば正しい答えを言ってくれる場合もありますがその場合でもそもそも指摘するためには言っていることが正しいかどうかを判別できるようにならなくてはいけません。また指摘しても間違う場合もあるし、指摘したことで正しかった部分が間違いに変わることもあります。
FAQ
chatGPTの出現によって数学者の仕事は奪われるのか？
これはNoだと思います。でもまあ仕事の内容が若干変わる可能性は否定できません。
昔は一生をかけて円周率を手計算した数学者もいたみたいですが、現在は計算機の出現によってその計算をする必要はなくなりました。しかし計算機が誕生したからといって数学者という職業はなくなりませんでした。人間はコンピュータの代わりに「計算機で計算できないこと」を計算するようになったからです。数式処理ソフトが出現したことで便利になりましたが、数式処理ソフトでもできない計算は多いのでその場合は代わりに人間がやることになりました。AIの出現によってどうなるかは、歴史を見れば傾向がわかるかもしれないですね。知らんけど
コンピュータ上で人間の脳が完全に再現できるようになったら変化は起きそう？
そもそもchatGPTに数学を聞くのが悪い
たしかに、そもそもchatGPTに数学はあまり向いてないかもしれないですね。
多少のガバは許しててへぺろというスタンスが厳密性を求める数学と相性が悪いのかもしれないです。
〇〇を検証してない！系
もちろん、この記事に書かれていることが全てではなく、他にも検証できそうなことはとても多そうです。また人間の手による情報の精査も大変そうに見えます。
こればかりは自分の能力の限界です。許して亭許して
プロンプトの打ち方が悪い！
そう言われると否定できないですね…
ググるにも技術が必要なように、もしかしたらプロンプトの構成にも技術が必要なのかもしれません。追試報告まってます。
一般のグラフに対して合成抵抗を求めるアルゴリズム
概要
たとえばこのような回路が与えられたとき、合成抵抗を求めるには、簡単な計算で求められるはずです。並列の部分は1/(1/R+1/R)=R/2で、直列のRと合わせることでR+R/2=3R/2となります。
次、
こんな感じになると今までの並列直列戦法ではうまくいきません。
まあでも立方体の場合はまだ良心的です。各辺に流れる電流を記録してみると、対称性からちゃんと計算できるので、こうなります。
Iの電流を流すと、RI/3+RI/6+RI/3=5R/6 Iの電位差が生じるので、結局5R/6の大きさの抵抗でもいいということなので、合成抵抗は5R/6となります。
ただ、今回はたまたま立方体に対称性があったから解けたのですが、一般のグラフのときでも解けるようなアドホックじゃない方法はあるのでしょうか？
問題設定
N頂点M辺の連結無向グラフがある。頂点には1からNまでの番号がついている。
また、各辺は大きさRの抵抗となっている。
頂点1と頂点Nで端子を結んだときの合成抵抗を求めよ
理論
こういう場合に使うのはキルヒホッフの法則です。
つまり、
・閉路を見たときに電位差の和は0
・分岐点を見たときに、入ってくる電流＝出ていく電流
です。
つまり、各辺ごとに流れる電流を変数として連立方程式を作って解けばOK
…としたいところですが、変数の数はMあります。また、プログラムを組むとき、「閉路の電位差の和=0」の部分の処理が面倒です。
なので、以下の方法にします。
閉路を見たときに電位差は0となっているため、各頂点に対して電位を定義することができます。これは辺ごとに見て、流れる電流×抵抗値の和を追跡すれば良いわけです。で、キルヒホッフの第2法則より、どのような経路で電位を計算しても最終結果がおなじになることが保証されているので問題ないわけです（電流の向きが追跡する向きと逆なら、電流の値に-1をかければOK）
で、$V_1,...,V_N$を拡頂点の電位の値とします。
こうして、$u\to v$の辺があったときはその辺に$u\to v$方向に大きさ$\dfrac{V_v-V_u}{R}$の電流が流れると考えればOKというわけです。そうすれば電位の値をどのように設定してもキルヒホッフの第2法則は確実にクリアできるようになっています。
で、実際の電位の値がどうなっているかについては、キルヒホッフの第1法則を使います。
頂点$u$をみたとき、$u$に隣接する辺の集合を$G_u$とします。
このとき、$u$に入ってくる電流-$u$から出ていく電流は、
$\sum_{v\in G_u} \dfrac{V_u-V_v}{R}$
となっています。これが0になる...と言いたいところですが、頂点1とNだけは例外でIと-Iになります。
百聞は一見にしかず
例題を示しましょう
こんなグラフがあったとしたら
$$\begin{pmatrix}2& -1& 0& -1& 0& 0\\-1& 3& -1& 0& -1& 0\\0& -1& 2& 0& 0& -1\\-1& 0& 0& 2& -1& 0\\0& -1& 0& -1& 3& -1\\0& 0& -1& 0& -1& 2&\\\end{pmatrix}\begin{pmatrix}V_1\\V_2\\V_3\\V_4\\V_5\\V_6\\\end{pmatrix}=\begin{pmatrix}1\\0\\0\\0\\0\\-1\\\end{pmatrix}$$
という連立方程式を解けば良いです。
ところで、この行列は一般に正則とはなりません。なぜなら右から($1,1,\ldots,1)^\top$を掛けると0になるからです。
ですが、恐らくですが、グラフが連結ならば連立方程式の解は一応存在します。解を求めるには
$$\begin{pmatrix}2& -1& 0& -1& 0& 0&1\\-1& 3& -1& 0& -1& 0& 0\\0& -1& 2& 0& 0& -1& 0\\-1& 0& 0& 2& -1& 0& 0\\0& -1& 0& -1& 3& -1& 0\\0& 0& -1& 0& -1& 2& -1\\\end{pmatrix}$$
のrrefを求めればOKです。
これはラプラシアン行列というものを基本として、一番右の列に1列値を追加したN行N+1列の行列となっています。
これを数式処理ソフトなどで計算すると
$$\begin{pmatrix}1& 0& 0& 0& 0& -1& 7/5\\0& 1& 0& 0& 0& -1& 4/5\\0& 0& 1& 0& 0& -1& 2/5\\0& 0& 0& 1& 0& -1& 1\\0& 0& 0& 0& 1& -1& 3/5\\0& 0& 0& 0& 0& 0& 0\\\end{pmatrix}$$
みたいな形になります。左からN列がこのような形になっていたらOKです。このとき一番右の列を見ると、i行目は頂点$V_i$と頂点$V_N$の電位差の値となっています。当然$V_N$から$V_N$への電位差は0なので、一番右の列の一番下の行は0となっている。
で、$V_1$から$V_N$へ電気を流したときの合成抵抗は行列の一番右上の値となっています。つまりこの例の場合だと$7R/5$というわけです。
この手法は一般のグラフに対しても適用することができます。
ソースコード
rrefを計算してくれるコードはそこら中に転がっているのでそれを使います。
例としてsympyにはrrefを計算してくれる関数があるみたいなのでそれに丸投げします。
gist04f592a5927e7833ca67c9e1e880003c
実行例
立方体のグラフの場合、こうなります
[ [1, 0, 0, 0, 0, 0, 0, -1, 5/6], [0, 1, 0, 0, 0, 0, 0, -1, 1/2], [0, 0, 1, 0, 0, 0, 0, -1, 1/2], [0, 0, 0, 1, 0, 0, 0, -1, 1/3], [0, 0, 0, 0, 1, 0, 0, -1, 1/2], [0, 0, 0, 0, 0, 1, 0, -1, 1/3], [0, 0, 0, 0, 0, 0, 1, -1, 1/3], [0, 0, 0, 0, 0, 0, 0, 0, 0]]
i xor jが2べきのときに辺が繋がっている状態だと思ってください。
ただ、行列の各成分は1からNに電流を流したときの頂点iと頂点Nの電位差となっているため、iとNを端子で結んだときの合成抵抗になってないことに注意してください。
立方体の同一平面上の対角線を端子にした場合だとこうなります。
ここで、入出力端子を変更するには一番右の列を変えればOKです。
G=[[1, 2, 4], [0, 3, 5], [3, 0, 6], [2, 1, 7], [5, 6, 0], [4, 7, 1], [7, 4, 2], [6, 5, 3]]
行列
[3, -1, -1, 0, -1, 0, 0, 0, 1]
[-1, 3, 0, -1, 0, -1, 0, 0, 0]
[-1, 0, 3, -1, 0, 0, -1, 0, 0]
[0, -1, -1, 3, 0, 0, 0, -1, -1]
[-1, 0, 0, 0, 3, -1, -1, 0, 0]
[0, -1, 0, 0, -1, 3, 0, -1, 0]
[0, 0, -1, 0, -1, 0, 3, -1, 0]
[0, 0, 0, -1, 0, -1, -1, 3, 0]
rref
[
[1, 0, 0, 0, 0, 0, 0, -1, 1/2],
[0, 1, 0, 0, 0, 0, 0, -1, 1/8],
[0, 0, 1, 0, 0, 0, 0, -1, 1/8],
[0, 0, 0, 1, 0, 0, 0, -1, -1/4],
[0, 0, 0, 0, 1, 0, 0, -1, 1/4],
[0, 0, 0, 0, 0, 1, 0, -1, 1/8],
[0, 0, 0, 0, 0, 0, 1, -1, 1/8],
[0, 0, 0, 0, 0, 0, 0, 0, 0]]
3/4
一番右の列を調整すると入力端子と出力端子を変更することができます。
このときの合成抵抗はA(N,in)-A(N,out)で計算できるので、A(8,0)-A(8,3)=1/2-(-1/4)=3/4となり、合成抵抗は3R/4となります。
FAQ
このプログラムは抵抗値の比が有理数の時しか使えないのでは？
その場合では、係数を調整すればOK
キルヒホッフの第1法則のところが
$$\sum_{v\in G_u} \dfrac{V_v-V_u}{R_{u,v}}=0$$
なので、$(u,u)$成分は$\sum_{v\in G_u}\dfrac{1}{R_{u,v}}$で、$(u,v)$成分は$-\dfrac{1}{R_{u,v}}$であるような行列に対して同様の連立方程式を解けばOKです。
2Ωの抵抗を再現するには1Ωの抵抗を2個直列に繋ぐことで一応再現できますが頂点数が増えます。（他にも有理数に対して適切なグラフを埋め込むことでなんとかできなくもないですが…）係数が有理数の場合でも行列のサイズを削減できて計算量を減らすことができます。
多重辺・自己ループでもいける？
一応行けます。例えばこの記事の最初で出てきた回路の場合、
G=[[1,1],[0,0,2],[1]]
とすればOKです。
自己ループも同じようなノリでいけなくはないですが…正直意味は無いと思います。
なぜならば、自己ループは両端の電位差がないため電流が流れません。なのであってもなくても全体の結果には影響しません。
計算量は？
この記事で上げたソースコードの場合、rrefを計算するところがボトルネックになっているのでそこに完全に依存しきってます
まあガウスの消去法なので計算量は多項式$O(N^3)$だと思います。
sympyって遅いのでしょうか？あまり使ったこと無いのでわかりませんごめんなさい
人の最大の力を競う数学の大会
人の最大の力を競う数学の大会、優勝してしまった…
— しゃかやみ (@shakayami_) 2023年3月11日
— しゃかやみ (@shakayami_) 2023年4月1日
匿名希望になってもうた pic.twitter.com/PKCkL70Gbe
— しゃかやみ (@shakayami_) 2023年4月1日
匿名希望はわたしです
問題
問1
(i)これはO(HW)のdp
実は斜め移動の回数を固定すると縦・横の移動係数も定まるので多項係数となる。結局$\min(H,W)$個くらいの多項係数の和になる。なので$1\leq H,W\leq 10^5,\mod 998244353$でもいけそう
(ii) (i)の答えが681と比較的少ないので、681回O(HW)のdpして足し合わせたらいけた
もっと効率のいい方法はわからなかった。
問2
(1) とりあえず愚直解を書く
したら規則性は見えた。つまり$(1+x+x^2+x^3+x^4+x^5+x^6+x^7+x^8+x^9)^n$を展開したときの$x^k$の係数になりそう
(2) 愚直にやったら$O(10^n)$だったけど、規則性が見えたので多項式時間のプログラムになった。なのでn=20とかも楽々に計算することができて、その結果をOEISにぶちこむと以下の数列が出てくる
説明文を見る限り、$O(n)$より計算量の低い表記は未判明っぽかったのでそれ以上の深追いはやめて$G_i$はシグマ表記が残る形にした。
$G_i$が最大になる$i$は$i=\lfloor \dfrac{9m+1}{2}\rfloor $であろうことは実験で察することができたけど証明は間に合わなかった…
問3
ゲーム系は苦手やねん…と思いながら見てたけど、よく見てみるとGrundy数でいけそう。
ここで、状態を$[i_l,i_r)\times [j_l,j_r)$という長方形領域でもって遷移するプログラムを書いた。全部先手必勝になって若干不安になった。
提出したあとで気づいたけど、チョコレートが欠けていない場合はある程度解析できた。
「山に$n$個の石があるときに$n/2$個まで石を取り除けて、操作できなくなったら負け」というゲームのGrundy数は実験してOEISにぶちこむとA025480 - OEISであることがわかるのだが、長方形になると全体のGrundy数は2つのGrundy数のXORとなる。なのでa(H)=a(W)なら後手必勝、そうでないなら先手必勝となる。A025480の第n項は$O(\log{n})$で計算できるので$O(\log{H}+\log{W})$で勝敗判定ができる。長方形なら多くの場合で先手必勝になりそう。後手必勝になるのは正方形の場合や、$n\times (2n+1)$や$n\times (4n+3)$、・・・$n\times (2^k n+(2^k - 1))$みたいな場合のときである。
余談だけど提出するファイル形式（ファイル名）を間違えているのに途中で気づいて時間を少しロスしてしまった。
問4
まず確率を計算するのは簡単にできる
問1 なんもわからんかったんでbit全探索した
問2 これもなんもわからんかったんでbit全探索…と言いたいところだが明らかに間に合わないのでどうしようかといったところ。確率の比の整数が単純だったらナップサックDPで通るけど比は単純じゃない。そうすると多項式時間が厳しそうな匂いがしてくる（今調べたけど部分和問題なのでNP完全。多項式時間は絶望的です）ところで、よく見てみると41回以内に終わるので半分全列挙が使えそうな気がする。なので書くと無事現実的な時間で終わるプログラムが書けた。
時間に余裕があったので、最小値を達成するようなパターンの数を計算するプログラムを書いた。
差の最小値が0になるのでバグってないか少々不安になった
解答
解答として提出したソースコードを公開しています。
賞金
アマギフ2万円
Wolfram Alpha Proの1年間ライセンス
なぜ匿名希望にしたのか
あまり覚えてない。多分参加登録したときに「名前を公開することに同意するか」というところで「同意しない」を答えたからだと思われる。
感想
競プロっぽかった
All Pair Digit Sums ARC158-C
アレが出てきた…！
なんとかコンテスト中に通せたので良かった。
問題概要
$f(x,y)$を$x+y$の桁和とする。このときに$\sum_{i,j} f(A_i,A_j)$を解けるだろうか？ただし$O(N^2)$は間に合わないよ
解法
まず、以下の等式が成り立つ
$$f(x)=x-9\sum_{n=1}^{\infty}\lfloor \dfrac{x}{10^n}\rfloor$$
$n$についての無限和になっているけど、実際には$x\geq 10^n $となるような範囲の$n$だけ計算すればOK
今回の場合$A_i+A_j\leq 2\times 10^{15}$なので$n\leq 16$まで計算すればOK
つまり、求める式はこうなる
$$\sum_{i=1}^{N}\sum_{j=1}^{N} (A_i+A_j)-9\sum_{n=1}^{\infty}\sum_{i=1}^{N}\sum_{j=1}^{N}\lfloor \dfrac{A_i+A_j}{10^n}\rfloor$$
ここで、
$$\sum_{i=1}^{N}\sum_{j=1}^{N} (A_i+A_j)=2N\sum_{i=1}^{N}A_i$$
なのでこの部分は$O(N)$で計算できる。
結局、以下の式を計算できればOK
$$F(M):=\sum_{i=1}^{N}\sum_{j=1}^{N}\lfloor \dfrac{A_i+A_j}{M}\rfloor$$
ところで、
$$G(M):=\sum_{i=1}^{N}\sum_{j=1}^{N}(A_i+A_j)\mod M $$
という式において、
$M\lfloor x/M\rfloor +(x\mod M)=x$なので、
$$F(M)=\dfrac{1}{M}\left(2N\sum_{i=1}^{N} A_i - G(M)\right)$$
である。
よって、$G(M)$が計算できればOKである。
ここで、
$$G(M)=\sum_{i=1}^{N}\sum_{j=1}^{N} (A_i+A_j)\mod M $$
について、
$$G(M)=\sum_{i=1}^{N}\sum_{j=1}^{N} ( (A_i\mod M)+(A_j\mod M) )\mod M $$
が成立する。よって$A_i \leftarrow A_i\mod M $と変換してから計算し直しても問題ない。
以下、$A_i$を$A_i\mod M $に変換したものとして書く。つまり、$0\leq A_i\lt M $である。
このとき、$(A_i+A_j)\mod M $は$A_i+A_j$または$A_i+A_j-M $と等しくなる。これは$0\leq A_i+A_j\lt 2M $より成り立つ。また、$(A_i+A_j)\mod M=A_i+A_j-M $となるのは$(A_i+A_j)\geq M $となるようなときである。
つまり、
$$G(M)=2N\sum_{i=1}^{N}A_i - M \#\{(i,j);A_i+A_j\geq M \}$$
となる。
問題は
$$\#\{(i,j);A_i+A_j\geq M \}$$
（つまり、$A_i+A_j\geq M $となるような$(i,j)$の組の個数）
をどう求めるかである。
結論から言うと、以下の方法を使えば$O(N\log{N})$で計算できる。
0. （ $A$の全要素を$M $で割ったあまりに変換したとする）
1. $A$を$A_i \mod M $でソートする。
2.i=1,...,Nについて以下の操作をする
$A_k\geq M-A_i$となるような最小の$k$を二分探索で探す。$i$に対して$j=k,k+1,k+2,...,N$のときだけ$A_i+A_j\geq M $となるのでその分を答えに加算する
以上の方法によって答えを計算することができた。
実装例
コードの中にsolve_naive,G_naive関数がありますが、それは$O(N^2)$解で愚直に計算したもので、ランダムテストケースで合致するかでデバッグを行っています。
